완전히 이해해서 기억하고 있는 것만 적겠음
0. 직선AB, 반직선AB, 선분AB : 서로 다른 두 점 AB를 지나는 직선을 직선AB라고 하고, 점A에서 다른 한점인 B를 향하여 한없이 뻗은 선을 반직선AB라고 하고, 직선AB에서 점A에서 점B까지의 부분을 선분AB라고 함.
1. 중점 : 선분AB위에 한 점 M이 있고 선분AM과 선분MB의 길이가 같을때 점M을 선분AB의 중점이라고 부름.
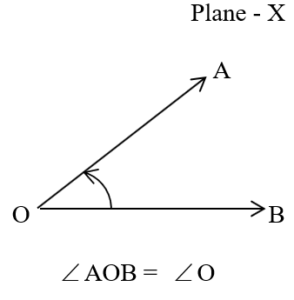
2. 각AOB : 점 O를 중심으로 한 두 반직선 OA와 OB가 이루는 도형을 각AOB라고 부름.
3. 각 AOB의 크기 : 반직선 OB가 점 O를 중심으로 다른 반직선 OA의 위치만큼 회전한 양을 각AOB의 크기라고 함.
4. 교각 : 두 직선이 한 점에서 교차할때 생기는 4개의 각을 교각이라고 부름.
5. 수직 : 두 직선의 교각이 직각(90도)일때 두 직선은 서로 수직한다고 함.
6. 수직이등분선 : 한 직선이 선분AB의 중점 M을 지나고, 이 직선이 선분AB에 대하여 수직할때 해당 직선을 선분AB의 수직이등분선이라고 부름.
7. 수선 : 두 직선이 수직할때 한 직선을 다른 한 직선의 수선이라고 부름.
8. 수선의 발 : 점p에서 떨어진 직선l에 수선을 그었을때 생기는 교점H를 점p에서 직선l에 내린 수선의 발이라고 부름.
쓰면서도 자기자신한테 놀라네
왜 네오만 오면 다 생각나냐;








 나도 공부한거 하루마다 올려봐야겠다
나도 공부한거 하루마다 올려봐야겠다





